Tengfei Wang , Jiubing Cheng , and Jianhua Geng
State Key Laboratory of Marine Geology, School of Ocean and Earth Science, Tongji University, Shanghai, China
Abstract:
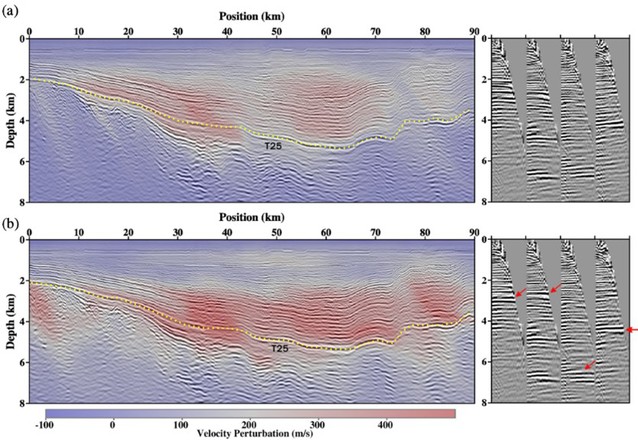
In controlled-source seismology, the standard full waveform inversion (FWI) can't reliably recover the macrovelocity structure in the deep part, if the surface seismic data lack of ultra-long offsets and very low frequencies. Reformulating the FWI for pre-critical reflections based on model scale separation leads to reflection waveform inversion (RWI), which aims to improve the reconstruction of low-to-intermediate model wavenumbers. However, the state-of-art RWI approaches rely on the gradient-type optimization, resulting in slow convergence and inaccurate recovery of the deep macrovelocities. Therefore, we present a Hessian-based second-order optimization in the context of RWI. Based on the reflection Fréchet derivative with respect to the background model, the approximate Hessian and the point spread functions (PSFs) on toy models with two and three layers are constructed to gain physical insights about parameter coupling and spatial resolution at the scale of low-to-intermediate wavenumbers for finite-offset and band-limited data. The high-velocity anomaly and checkerboard experiments demonstrate the benefit of incorporating the inverse approximate Hessian effect on the functional gradient. Accordingly, for large-scale applications, we propose a matrix-free Gauss-Newton RWI approach, in which the Hessian-vector product is formulated with the second-order adjoint-state method and an optimal updating direction is estimated in the nested inner loop to accelerate the convergence. A synthetic example and an application to the real data from East China Sea demonstrate that the proposed method can improve velocity model building and seismic imaging, especially for the deep targets.
Full Article:https://agupubs.onlinelibrary.wiley.com/doi/full/10.1029/2021JB022135